Um espaço lúdico da matemática e para a matemática mas onde o exercício livre da opinião e crítica é condição primordial. Aberto a ouvir, opinar, criticar e ser criticado...
Truques de matemática
segunda-feira, 18 de fevereiro de 2008
LABORATÓRIO DE MATEMÁTICA


Um espaço para a aprendizagem experimental da Matemática
As actividades de investigação em sala de aula tomaram, nos últimos anos, um papel fundamental tendo em conta as profundas alterações nos currículos de Matemática que apontam para a inovação nas finalidades e nos objectivos, conteúdos e metodologias, e na avaliação do ensino-aprendizagem. Na medida em que permite o confronto de ideias entre os alunos, bem como a exploração de tarefas e materiais na sala de aula, a implementação de actividades de exploração constitui uma inovadora perspectiva curricular. Os conceitos matemáticos inerentes ao currículo são mais facilmente e mais eficazmente interiorizados pelos alunos mediante a realização de actividades de investigação na sala de aula, seleccionadas orientadas estrategicamente pelo professor, visto que lhes é dada a oportunidade de por si só explorarem esses mesmos conceitos e chegarem às conclusões “pelo seu próprio pé”. Os conceitos introduzidos e explorados segundo esta abordagem tendem a ser interiorizados de uma forma natural e eficazmente duradoura.
Os saberes são construídos a partir da experiência, da reflexão e da prova; gradualmente, da intuição até à dedução. Privilegia-se a comunicação e a investigação, não ficando apenas por tarefas rotineiras. Em suma, trata-se, também, de adequar a educação escolar à evolução da sociedade. Porém, muitas vezes a gestão de espaços educativos e recursos materiais nas escolas não é a mais adequada. Prevalece ainda o espaço da aula de Matemática, apenas com mesas, cadeiras e o quadro de giz, na forma tradicional, e (nem sempre) um retroprojector. Incompreensivelmente, nos nossos dias, projectam-se e constroem-se escolas que dispõem dos já habituais espaços específicos (gimnodesportivos e salas artísticas, técnicas e laboratoriais), mantendo as salas "normais" para as restantes disciplinas. Estas dispõem de poucos materiais didácticos, geralmente guardados em armários ou arrecadações, longe das salas de aula.
Actualmente, tendo em conta tanto as referidas dificuldades como também a inexistência de espaços próprios para o trabalho interdisciplinar, muitas escolas começam agora a implantar o Laboratório de Matemática, ao abrigo do Plano de Acção para a Matemática (PAM). Este espaço é o ponto de partida para um ou mais espaços específicos para o ensino-aprendizagem da Matemática. Chama-se "laboratório", apenas porque se tornou usual esta designação: por um lado, a componente experimental da Matemática é diferente da das outras ciências; por outro, o referido espaço não se deve reduzir a actividades laboratoriais.
Algumas escolas continuam, ainda, a adquirir materiais já conhecidos e já explorados pelos alunos (em anos anteriores), quer através de projectos próprios quer por equipamento do Ministério. No entanto, verifica-se que alguns dos materiais, mesmo assim, não são utilizados, algumas vezes por desconhecimento de todas as suas potencialidades outras por dificuldades de utilização. Por outro lado, a utilização da tecnologia, embora recomendada em todos os níveis de ensino é, ainda, embrionária. Há, por isso, a necessidade de se encontrar conexões e produzir tarefas para aplicar em situações de aula e fomentar o uso das novas tecnologias e de materiais manipuláveis, num universo de interdisciplinaridade, uniformizando e optimizando os diversos recursos materiais.
domingo, 17 de fevereiro de 2008
A tabuada e a calculadora


Um texto de Nuno Crato
(Expresso, Dezembro de 2004)
Num conto magnífico incluído na colecção Nove Amanhãs, Isaac Asimov (1920-1992) imagina uma civilização do futuro que se tinha esquecido da tabuada e dos algoritmos das quatro operações. Apenas as máquinas conseguiam fazer contas. Os humanos tinham de as usar para todos os cálculos, mesmo os mais elementares.
Ninguém se interrogava sobre o que as calculadoras faziam. Mas, a certa altura, aparece um jovem técnico que começa a ficar curioso. Repara em certas regularidades e constrói uma tabuada. Pouco a pouco, percebe o mecanismo das operações e começa a fazer contas.
Afirma com toda a confiança: «Três vezes sete, vinte e um... quatro vezes oito, trinta e dois...». Os amigos duvidam e vão verificar os resultados com a máquina. Dá certo! Dá sempre certo! «Soma agora 23 com 48! Dá 71! E não é que dá mesmo!?»
A história foi escrita em 1958 e parece premonitória. De facto, há hoje muitos jovens estudantes que sacam das máquinas para resolver as operações mais elementares. Habituaram-se a isso quando estavam na escola e já não o sabem fazer de outra maneira. Ora, fazer contas mentalmente é muito útil no dia-a-dia. Serve para comparar preços no supermercado, fazer trocos, medir o tempo, deitar contas à vida.
Mas há ainda mais, conforme ficou claro para os muitos que na semana passada encheram as salas da livraria Almedina. Numa das habituais sessões do livro científico das «Sextas às Sete» dessa livraria, em Lisboa, Alexandre Castro Caldas explicou que o exercício do cálculo mental e a memorização, nomeadamente da tabuada, ajudam a desenvolver regiões do próprio cérebro e capacitam os jovens para outras actividades. Explicou também que há uma janela de oportunidade para essa aprendizagem. Privá-los desse treino em tenra idade é limitá-los no seu desenvolvimento intelectual futuro.
É o que se está a passar com muitos jovens. E a culpa não é deles. Com pretexto na «aprendizagem significativa», atacaram-se os «vícios da memorização», mas errou-se no alvo.
Leia-se o programa de Matemática do 1º Ciclo, aprovado em 1990. Diz-se aí que a «máquina de calcular não pode deixar de ter lugar no 1º Ciclo» (jovens dos seis aos dez anos). Fala-se nos «cálculos obtidos, utilizando algoritmos ou a máquina de calcular» e depois diz-se que «na sala de aula deve haver materiais de apoio e o professor permitirá que cada criança utilize, com liberdade, o que lhe for mais conveniente». Ou seja, diz-se que o professor não pode impedir uma criança de seis a dez anos de usar a calculadora sempre que ela o queira fazer. Ideia semelhante repete-se no «Currículo Nacional do Ensino Básico: Competências Essenciais» (2001), página 60.
Felizmente, a maioria dos professores tem mais bom senso que os teóricos da pedagogia romântica e sabe que permitir que o aluno use a máquina de calcular sempre que o queira é caminho certo para que ele nunca desenvolva o cálculo mental.
Dito tudo isto, é preciso acrescentar que a calculadora devia ser mais usada no Ensino Secundário. Sobretudo, mais bem usada. Nessa altura, começam a aparecer frequentemente contas muito difíceis, impossíveis de resolver manualmente. É preciso conhecer melhor a máquina de calcular para poder enfrentar esses novos desafios. Mas há muitos alunos que chegam à universidade sem saber calcular exponenciais, logaritmos ou tangentes, pois nunca perceberam as correspondentes funções das suas máquinas. É triste, mas por vezes parece que andamos a fazer tudo ao contrário.
Ilusões de óptica
As ilusões de óptica mostram figuras ambíguas, onde a percepção do nosso cérebro muda muito rapidamente, sem que haja qualquer alteração naquilo que é visto pelos nossos olhos.
Na sua forma mais simples, uma percepção ilusória mostra duas ou mais figuras que "encaixam" uma na outra.
Estas imagens foram tornadas famosas por M. C. Escher, embora o exemplo seguinte tenha sido introduzido por Edgar Rubin em 1915, antes de Escher.

O tipo mais divertido de ambiguidade através de desenhos é a ambiguidade dos "desenhos rivais". Neste tipo de ilusão, os diferentes desenhos estão contidos no mesmo espaço, mas dependendo da forma como a nossa mente interpreta as formas e linhas dominantes, assim se verá uma ou outra imagem, num dado momento.
De seguida, mostram-se mais alguns exemplos.
Nesta figura, vê um velho ou um rapaz novo?

E nesta figura, encontra um saxofonista ou um rosto feminino?

Aqui, temos um esquimó ou um índio?

Na sua forma mais simples, uma percepção ilusória mostra duas ou mais figuras que "encaixam" uma na outra.
Estas imagens foram tornadas famosas por M. C. Escher, embora o exemplo seguinte tenha sido introduzido por Edgar Rubin em 1915, antes de Escher.

O tipo mais divertido de ambiguidade através de desenhos é a ambiguidade dos "desenhos rivais". Neste tipo de ilusão, os diferentes desenhos estão contidos no mesmo espaço, mas dependendo da forma como a nossa mente interpreta as formas e linhas dominantes, assim se verá uma ou outra imagem, num dado momento.
De seguida, mostram-se mais alguns exemplos.
Nesta figura, vê um velho ou um rapaz novo?

E nesta figura, encontra um saxofonista ou um rosto feminino?

Aqui, temos um esquimó ou um índio?

sábado, 16 de fevereiro de 2008
Leituras Matemáticas - Martin Gardner
(Colecção O Prazer da Matemática)





Estes são alguns dos livros de Martin Gardner editados em Português pela Gradiva. Fazem parte de uma interessante colecção intitulada "O Prazer da Matemática", que é integrada por diversos livros de autores portugueses e estrangeiros onde podemos aprender um pouco de matemática de forma divertida e lúdica.
Nestes livros podes encontrar jogos, charadas, enigmas, truques, e muitas outras coisas que te farão sentir o prazer da matemática! São portanto uma óptima opção para os teus tempos livres e para partilhares com os teus amigos! Além dos livros aqui apresentados (entre eles, "Matemática Magia e Mistério", "O Festival Mágico da Matemática" e "Rodas, Vida e Outras Diversões Matemáticas") existe ainda um sexto intitulado "Ah, Apanhei-te!" do mesmo autor.
Martin Gardner - O Jornalista Matemático

Martin Gardner é uma das personalidades com maior destaque na área da matemática "recreativa" e a influência do seu trabalho é inquestionável. É autor de mais de 65 livros e inúmeros artigos que abrangem não só a matemática, mas também outras áreas tão diversas como a ciência, a filosofia, a literatura ou a magia. No entanto, Gardner não tem formação matemática e descreve-se a si próprio como um jornalista que escreve sobretudo acerca de matemática e de ciência e também de alguns outros campos de interesse.
Nasceu nos Estados Unidos da América, a 21 de Outubro de 1914, na cidade de Tulsa, situada no estado de Oklahoma. O seu pai era um geólogo e produtor de petróleo. Em 1936 formou-se em Filosofia na Universidade de Chicago e de seguida começou a trabalhar como repórter no jornal “Tulsa Tribune”.
Ainda antes da Segunda Guerra Mundial, durante a qual trabalhou ao serviço da Marinha, integrou o Departamento de Relações de Imprensa da Universidade de Chicago. No final da Guerra, regressou a Chicago onde iniciou a sua carreira como escritor freelancer, escrevendo pequenas histórias para a revista "Esquire".
De seguida, mudou-se para Nova Iorque onde colaborou durante oito anos na edição da revista "Humpty Dumpty’s". Em 1956 iniciou a edição mensal da coluna “Mathematical Games” na conceituada revista "Scientific American". A partir daí tornou-se mundialmente reconhecido e respeitado e passou inclusivamente a corresponder-se frequentemente com vários matemáticos.
Martin Gardner apresenta uma extraordinária capacidade para transmitir a essência de conceitos matemáticos sofisticados a uma vasta audiência e não apenas ao público com formação matemática.
Os conteúdos abrangidos nos seus livros e artigos ultrapassam os domínios tradicionais da matemática. Gardner interessou-se, por exemplo, pelo estudo de vários enigmas e jogos matemáticos e também pela magia, em particular pelos truques baseados na matemática, e chegou a desmascarar alguns charlatães que afirmavam possuir capacidades sobrenaturais.
A influência de Martin Gardner é tão grande que parte dos seus leitores e "fans" já organizaram várias conferências para trocarem impressões acerca da sua obra e existe também um asteróide que, em sua honra, foi designado por Gardner.
Actualmente vive na cidade de Norman, no estado de Oklahoma.





Estes são alguns dos livros de Martin Gardner editados em Português pela Gradiva. Fazem parte de uma interessante colecção intitulada "O Prazer da Matemática", que é integrada por diversos livros de autores portugueses e estrangeiros onde podemos aprender um pouco de matemática de forma divertida e lúdica.
Nestes livros podes encontrar jogos, charadas, enigmas, truques, e muitas outras coisas que te farão sentir o prazer da matemática! São portanto uma óptima opção para os teus tempos livres e para partilhares com os teus amigos! Além dos livros aqui apresentados (entre eles, "Matemática Magia e Mistério", "O Festival Mágico da Matemática" e "Rodas, Vida e Outras Diversões Matemáticas") existe ainda um sexto intitulado "Ah, Apanhei-te!" do mesmo autor.
Martin Gardner - O Jornalista Matemático

Martin Gardner é uma das personalidades com maior destaque na área da matemática "recreativa" e a influência do seu trabalho é inquestionável. É autor de mais de 65 livros e inúmeros artigos que abrangem não só a matemática, mas também outras áreas tão diversas como a ciência, a filosofia, a literatura ou a magia. No entanto, Gardner não tem formação matemática e descreve-se a si próprio como um jornalista que escreve sobretudo acerca de matemática e de ciência e também de alguns outros campos de interesse.
Nasceu nos Estados Unidos da América, a 21 de Outubro de 1914, na cidade de Tulsa, situada no estado de Oklahoma. O seu pai era um geólogo e produtor de petróleo. Em 1936 formou-se em Filosofia na Universidade de Chicago e de seguida começou a trabalhar como repórter no jornal “Tulsa Tribune”.
Ainda antes da Segunda Guerra Mundial, durante a qual trabalhou ao serviço da Marinha, integrou o Departamento de Relações de Imprensa da Universidade de Chicago. No final da Guerra, regressou a Chicago onde iniciou a sua carreira como escritor freelancer, escrevendo pequenas histórias para a revista "Esquire".
De seguida, mudou-se para Nova Iorque onde colaborou durante oito anos na edição da revista "Humpty Dumpty’s". Em 1956 iniciou a edição mensal da coluna “Mathematical Games” na conceituada revista "Scientific American". A partir daí tornou-se mundialmente reconhecido e respeitado e passou inclusivamente a corresponder-se frequentemente com vários matemáticos.
Martin Gardner apresenta uma extraordinária capacidade para transmitir a essência de conceitos matemáticos sofisticados a uma vasta audiência e não apenas ao público com formação matemática.
Os conteúdos abrangidos nos seus livros e artigos ultrapassam os domínios tradicionais da matemática. Gardner interessou-se, por exemplo, pelo estudo de vários enigmas e jogos matemáticos e também pela magia, em particular pelos truques baseados na matemática, e chegou a desmascarar alguns charlatães que afirmavam possuir capacidades sobrenaturais.
A influência de Martin Gardner é tão grande que parte dos seus leitores e "fans" já organizaram várias conferências para trocarem impressões acerca da sua obra e existe também um asteróide que, em sua honra, foi designado por Gardner.
Actualmente vive na cidade de Norman, no estado de Oklahoma.
Queres ser um adivinho?...
Pede a alguém conhecido para escolher de dentro de uma caixa de dominó uma peça qualquer. Dá-lhe as seguintes instruções (para perceberes melhor segue o nosso exemplo):
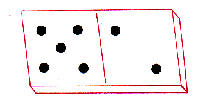
Multiplica o maior número por 5. [5 x 5 = 25]
Adiciona 8. [25 + 8 = 33]
Multiplica por 2. [33 x 2 = 66]
Adiciona o número menor da peça de dominó. [66 + 2 = 68]
Depois do teu amigo ter feito todas as contas, pergunta-lhe o resultado final a que chegou. ( No caso do nosso exemplo ele diria 68 ).
Subtrai 16 a esse valor. [68 -16 = 52]
Finalmente diz-lhe que os números da peça de dominó que ele escolheu são o 5 e o 2.
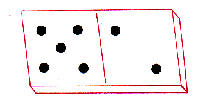
Multiplica o maior número por 5. [5 x 5 = 25]
Adiciona 8. [25 + 8 = 33]
Multiplica por 2. [33 x 2 = 66]
Adiciona o número menor da peça de dominó. [66 + 2 = 68]
Depois do teu amigo ter feito todas as contas, pergunta-lhe o resultado final a que chegou. ( No caso do nosso exemplo ele diria 68 ).
Subtrai 16 a esse valor. [68 -16 = 52]
Finalmente diz-lhe que os números da peça de dominó que ele escolheu são o 5 e o 2.
domingo, 10 de fevereiro de 2008
Problemas para pensar

1º Problema
OS SALTOS DOS MENINOS E DAS MENINAS

Alguns meninos e meninas estavam a saltar à corda no recreio e a contar quantas vezes seguidas cada um deles conseguia saltar. Tenta calcular quantos saltos deu cada menina e menino.
1. A Joana saltou menos oito vezes do que a Carolina
2. Juntas, a Daniela e a Rute saltaram 37 vezes
3. O João deu mais oito saltos do que a Daniela
4. A Joana e a Daniela têm uma diferença de apenas três saltos
5. Os saltos da Carolina ultrapassaram os da Daniela em cinco.
2º Problema
VAMOS CONTAR PATAS ?


Numa quinta existem perus e coelhos:
Ao todo são 26 cabeças e 70 patas.
Quantos são os perus e quantos são as coelhos?
3º Problema
OS ANIMAIS DA JOANA...

A Joana tem 7 animais de estimação. Possui cães e gatos. Cada cão come 5 biscoitos por dia e cada gato 4. A Joana tem de comprar 32 biscoitos por dia.
Quantos cães e quantos gatos tem a Joana?
4º Problema
OS APERTOS DE MÃO

Quinze cavaleiros foram convidados para uma refeição sumptuosa no castelo de Guimarães. Antes de se sentarem, cada um dos quinze cavaleiros apertou a mão a todos os outros.
Quantos apertos de mão houve?
sexta-feira, 1 de fevereiro de 2008
Subscrever:
Mensagens (Atom)









